Introduction to Optics

Name of the course	Online	Lecture	Exercises	Lab
Optics and Photonics	✓	✓	✓	✗

Context

Preliminary courses/knowledge:

• Mathematics at university level
• Programming (with Matlab) at average level

Recommended Preliminary courses:

• Fundamentals of Physics or Electrical Engineering [w3]

Follow-on courses:

• Silicon Photonics Laboratory [w3]
• Electromagnetic Simulation Laboratory [w3]

Details

The course Optics and Photonics introduces the basic theory of optics as shown in the table below. Students get introduced to the basic concepts in the theoretic part and work on calculation and programming exercises in the practical part of the course. Each student will to give a 5-10 min talk on one of the topics shown in the table.

Course Records

Modules	Content	Lecture	Exercise
	Student Guidance	[TBD]
1	History of Optics	[PDF]	[PDF]
1	Electromagnetic theory of light	[PDF]	[PDF]
2	Light and matter	[PDF]	[PDF]
3	Electromagnetic energy	[PDF]	[PDF]
4	Ray optics	[PDF]	[PDF]
5	Fourier optics	[PDF]	[PDF]
6	Diffraction theory	[PDF]	[PDF]
7	Fourier simulation methods	[PDF]	[PDF]
8	Finite difference approximation methods	[PDF]	[PDF]
9	The FDTD method	[PDF]	Lab*
10	Silicon photonics	[PDF]	Lab*

* lab exercise on the FDTD and VWPM method using the free simulators MEEP and VWPM

Essays

No.	Title	PDF
1	Theory of waves	[PDF]
2	Paraxial Helmoltz equation	[PDF]
3	Approximation of the material equations	[PDF]
4	Dispersion equation from newtonian mechanics	[PDF]
5	Energy flux	[PDF]
6	Local and total absorption	[PDF]
7	Electromagnetic waves in metals	[PDF]
8	Vector field in single layer	[PDF]
9	Planar and spherical mirror	[PDF]
10	Resolution criteria of imaging systems	[PDF]
11	Cylindrical aperture function	[PDF]
12	Fraunhofer diffraction	[PDF]
13	Geometric construction of single slit diffraction patterns	[PDF]
14	Free space propagation and Weyl's formula	[PDF]
15	Debye theory	[PDF]
16	Electromagnetic scattering	[PDF]
17	Fresnel and Fraunhofer approximation from rigorous diffraction theory	[PDF]

Example: Grin Lens vs. Spheric Lens

Matlab exercises

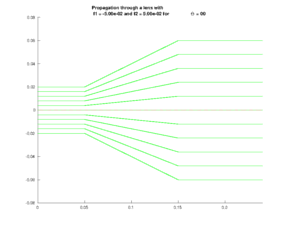Ray propagation can be described with the ABCD-matrix paradigm where a linear propagation is assumed in alignment with ray optics. Students develop Matlab code to simulate propagation through homogeneous media and lenses of various types. The relevant transformation matrices are introduced in the lectures.

Students analyse propagation paths and the formation of images. The correspondence of a pupil function (limit the aperture) to the depth of focus and the intensity of image points examined.

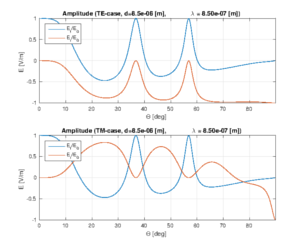
Reflectivity, Transmittivity and Absorptance is analysed with Matlab. Students program Matlab to simulate the energy characteristics of a single layer Fabry-Perot resonator from an infinite number of reflections and draw the characteristic curves. The correspondence of the curves to anti-reflection coatings, coatings with maximum transmission and absorption is investigated.

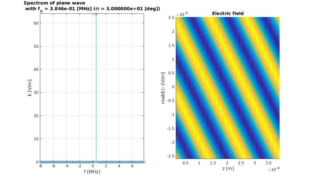
The correspondence of spatial frequencies to angles of propagation is investigated with Matlab. Students are trained to interpret the spectrum of electromagnetic field distributions and understand the theory in context of image filtering. The exercise provides the foundation for Fourier-based simulation methods like the Beam Propagation Method, Wave Propagation Method and the Vector Wave Propagation Method.

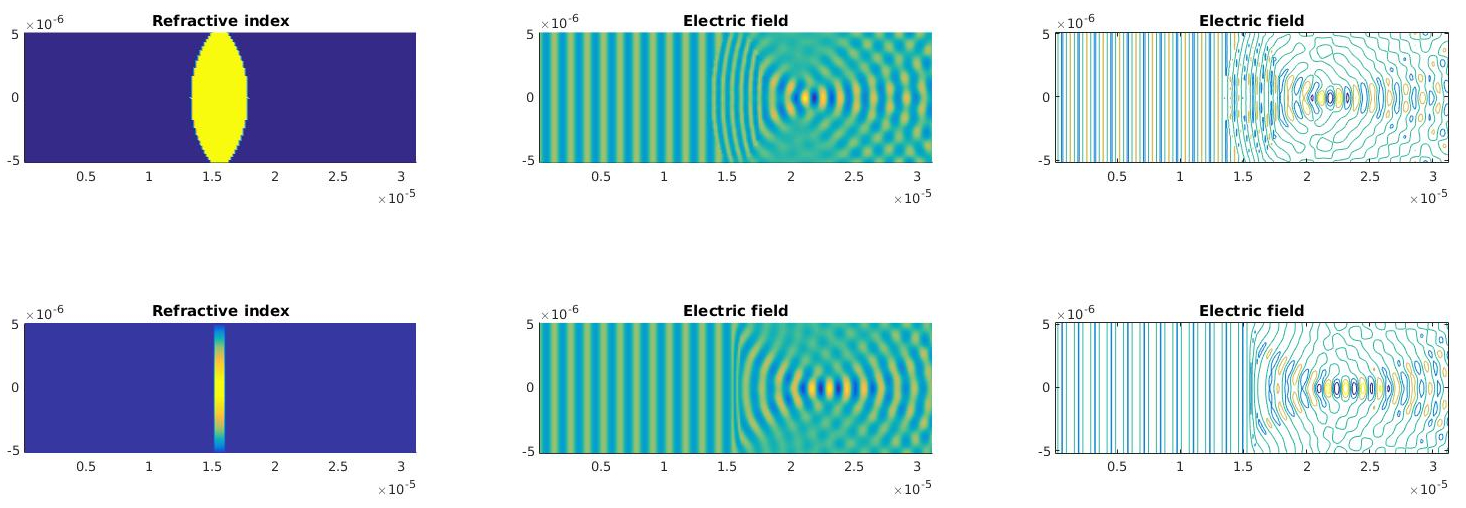
Spectral analysis of field distributions like Gaussian beams shows that propagated field distributions are obtained from a propagation of modes. Students program a two-dimensional scalar version of the WPM and BPM. The code will be extended to simulate the propagation of electromagnetic scalar waves through lens systems. Students are encouraged to extend the scalar version to the vector version and the two-dimensional to a three-dimensional version but this is advanced and not part of the regular course content.

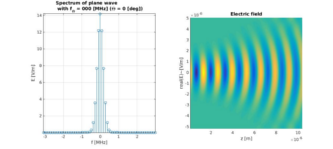
Matlab, C/C++ and Delphi sources for three-dimensional, vector and bidirectional propagation are available and will be used to compare the results from FDTD to the results from Fourier-based simulators and perform a mode analysis. Preliminaries for the Matlab exercises are a base knowledge and experience in programming with Matlab. Simulink is not needed in this context.

Literature

[1] Principles Of Optics, Born & Wolf, Cambridge University Press, ISBN 0-521-64222-1
[2] Fourier Optics, Goodman, Roberts Publ., ISBN 0-974-70772-4
[3] The Finite-Difference Time-Domain Method, Taflove, Artech House Inc., ISBN 1-580-53832-0
[4] Engineering Optics With Matlab, Poon & Kim, World Scientific Publ. Co, ISBN 9-789-812-56873-1
[5] Optics, Hecht, Addison-Wesley Publ., ISBN 9-780-805-38566-3