Modelling and control of industrial processes

Industrial processes are automated and controlled to secure proper operation conditions in terms of safety, economy and compliance with environmental regulations. To obtain a maximum output at minimum cost, the modeling and control algorithms need to be precise and fast enough to react on changes in operation conditions.

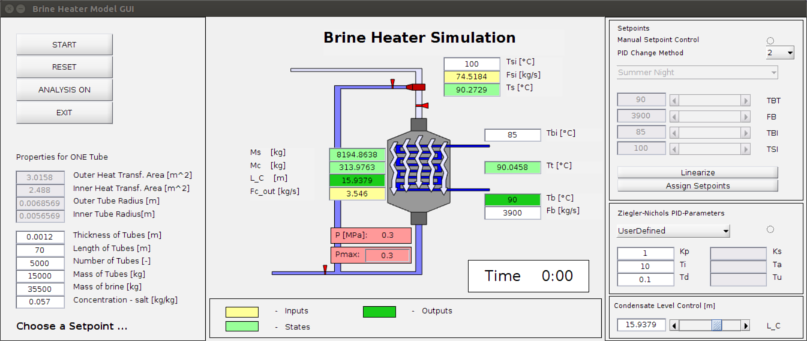
The brine heater of a desalination plant deter- mines the brine temperature to be delivered to the compression units. At the right temperature, a maximum of desalted water is obtained. The brine is supposed to flash out under decreasing pressure conditions in the multiple compression stages of the plant. The brine temperature decreases while flowing down the multiple stages and so does the boiling temperature due to decreasing pressure in the chambers. Thereby a series of flash-outs secures a maximum amount of desalted water.

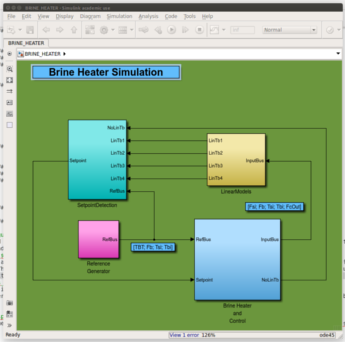
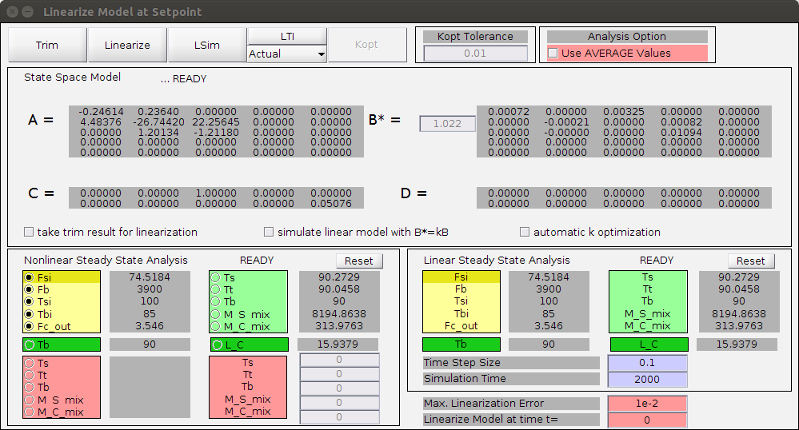
The process is modelled with Matlab using Simulink building blocks and m-files. The nonlinear model is formulated in an s-function and simulated using the ODE45 solver. The process is controlled at four pre-defined setpoints, corresponding to environmental conditions for day and night in summer and winter. The nonlinear model is linearized and a linear PID control is applied to each of the setpoints. To support a bumpless transfer between the setpoints, a Lyapunov cost function on the control error is minimized in an anti-integration windup control scheme.

Simulation results show that a bumpless transfer is achieved with this hybrid control algorithm. The model advances in realtime and all parameters can be observed during processing. A manual setpoint control is supported, maintaining the ability of bumpless transfer. The brine level can be manipulated in realtime, observing how the control adapts to the changed conditions and maintains the expected brine temperature. It is secured by control that the top brine temperature is never exceeded, preventing damage to the plant and its operators.

Thermophysical properties of water and steam

The model utilizes tables for thermophysical properties of water and steam recommended by the International Association for the Properties of Water and Steam IAPWS-IF07.

The properties are set for four regions which set the conditions for the properties like temperature and pressure..

PID controller

The linearized models are controlled by a Ziegler-Nichols PID controller with Anti-Integration-Windup option to support bumpless transfers between setpoint. A Lyapunov function is utilized to determine timing for a change of the setpoint.

Differential equations

The state transfer model is formulated with five differential equations defining the time derivatives of five corresponding states, steam temperature, tube temperature, brine temperature, mass of steam and mass of brine exposed to steam.

[1] A. Gambier, M. Fertig, E. Badreddin, "Hybrid modelling for supervisory control purposes for the brine heater of a multi stage flash desalination plant.", In Proceedings of the 2002 American Control Conference 6. 2002, 5060-5065.
[2] A. Gambier, M. Fertig, E. Badreddin, "Hybrid supervisory control of the brine heater for multistage flash desalination plants", In Proceeding of the 15th IFAC World Congress (IFAC 2002). 2002.
[3] A. Gambier, M. Fertig, E. Badreddin, "Hybrid modelling and control of the brine heater in multi-stage flash desalination plants", 2nd World Conference on Technology Advances for Sustainable Development and Renewable Energy Workshop (MCEET), Cairo, Egypt 2002.
[4] A. Gambier, E. Badreddin, "Application of hybrid modeling and control techniques to desalination plants, Desalination, Volume 152, Issues 1–3, 10 February 2003, Pages 175-184.
[5] A. Gambier, E. Badreddin, "Dynamic modelling of MSF plants for automatic control and simulation purposes: a survey, Desalination Volume 166, 15 August 2004, Pages 191-204.
[6] A. Gambier, E. Badreddin, "Dynamic modeling of a single-stage MSF plant for advanced control purposes", Published in the Proceedings of 2005 IEEE Conference on Control Applications, 2005. CCA 2005.

Kinematic control of an autonomous mobile robot with analogical gates*

The concept of behavioral control intends to combine a set of behaviors to complete a task. In the shown example, a mobile robot with non-holonomic constraints is supposed to reach a target coordinate without colliding with obstacles. The attractive force towards the goal is merged with the repulsive force from sensor information to avoid collisions with obstacles by using analogical gates.

The shown simulation is obtained from behavior fusion and programmed with Matlab. The plots are captured and combined to an animated gif file. The simulation visualizes that the concurring behaviors 'reach the target coordinate' and 'do not collide with obstacles' override each other, dependent on the position of the robot.

The right side of the animation shows how the mobile robot perceives its environment from simulated on-board ultrasonic sensors. The ultrasonic sensors are implemented by a simplified model of concentric lines with equidistant angle-separation originating from the robot position and intersecting with obstacles or the scene boundary.

The trajectory shows that if the target coordinate cannot be reached due to kinematic or environmental limitations, the control approach might seek supervisory assistance or accept a position deviation to avoid circulating around the target coordinate. This supervisory control needs to be managed by for example a higher level of a recursive nested behavior control structure.

*Principles and Applications of Analogical Gates in the Control of a non-holonomic Autonomous Mobile Robot.
*Analogical gates: a network approach to fuzzy control with applications to a non-holonomic autonomous mobile robot.

Prof. Dr. Matthias Fertig